本节书摘来异步社区《贝叶斯方法：概率编程与贝叶斯推断》一书中的第1章，第1.8节，作者：【加】Cameron Davidson-Pilon（卡梅隆 戴维森-皮隆），更多章节内容可以访问云栖社区“异步社区”公众号查看。

1.8答案

1．计算后验的均值（即后验的期望值），我们只需要用到样本和a.mean函数。

print lambda_1_samples.mean()print lambda_2_samples.mean()```2．给定两个数a 和 b，相对增长可以由 (a − b)/b给出。在我们的实例中，我们并不能确定λ1和λ2的值是多少。通过计算

(lambda_2_samples-lambda_1_samples)/lambda_1_samples`

relative_increase_samples = (lambda_2_samples-lambda_1_samples)                                   /lambda_1_samplesprint relative_increase_samples[Output]:　[ 0.263 0.263 0.263 0.263 ..., 0.1622 0.1898 0.1883 0.1883]figsize(12.5,4)plt.hist(relative_increase_samples, histtype='stepfilled',           bins=30, alpha=0.85, color="#7A68A6", normed=True,           label='posterior of relative increase')plt.xlabel("Relative increase")plt.ylabel("Density of relative increase")plt.title("Posterior of relative increase")plt.legend();

为了计算这个均值，需要用到新向量的均值：

print relative_increase_samples.mean()[Output]:　0.280845247899```
    
     
    
3．如果已知 τ < 45，那么所有样本都需要考虑到这点：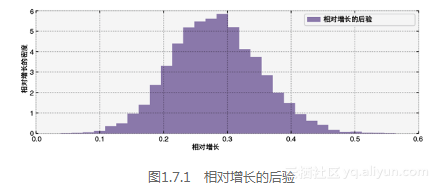

ix = tau_samples < 45

[Output]: